§7.9
二次曲面
三元二次方程所表示的曲面称着二次曲面。相应地，将平面叫做一次曲面。
一般的三元方程
所表示的曲面形状，已难以用描点法得到，那未怎样了解它的形状呢?
利用坐标面或用平行于坐标面的平面与曲面相截，考察其交线( 即截痕 )的形状，然后加以综合，从而了解曲面的全貌，这种方法叫做截痕法。
下面，我们用截痕法来讨论几个特殊的二次曲面。
一、椭球面
由方程
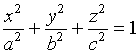(1)
所表示的曲面叫做椭球面。
1、由(1)可知：
这表明：椭球面(1)完全包含在以原点为中心的长方体内，这长方体的六个面的方程为
其中常数
叫做椭球面的半轴。
2、为了进一步了解这一曲面的形状， 先求出它与三个坐标面的交线
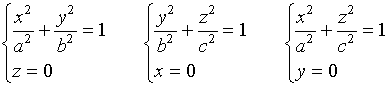
这些交线都是椭圆。
3、用平行于
坐标面的平面
去截椭球面，其截痕(即交线)为
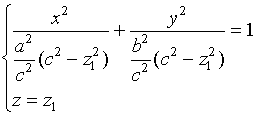
这是位于平面
内的椭圆，它的两个半轴分别等于
与
，其椭圆中心均在
轴上，当
由
渐增大到
时， 椭圆的截面由大到小，最后缩成一点。
4、以平面 
或 
去截椭球面分别可得与上述类似的结果。
综上讨论知：椭球面(1)的形状如图所示。
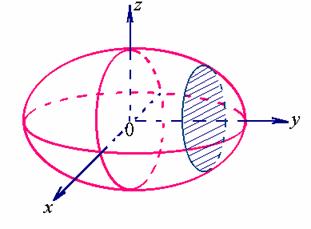
5、特别地，若
，而
，则 (1) 变为
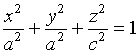
这一曲面是
坐标面上的椭圆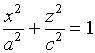 
绕轴旋转而成的旋转曲面，因此，称此曲面为旋转椭球面。
它与一般椭球面不同之处在于
如用平面与旋转椭球面相截时，所得的截痕是圆心在轴上的圆
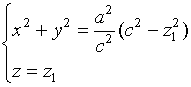
其半径为。
6、若 
，那未(1)变成
这是球心在原点，
半径为
的球面。
二、抛物面
由方程
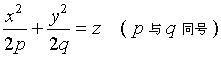(2)
所表示的曲面叫做椭圆抛物面。
设
， 用截痕法来考察它的形状
1、用坐标面
与该曲面相截，其截痕为
2、用平行于坐标面的平面
与该曲面相截，所得截痕为
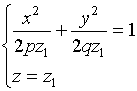
这是中心在轴， 半轴分别为
与 
的椭圆。
另外，平面
与该曲面不相交，因此，原点是该曲面的顶点。
3、用坐标面
与该曲面相截， 其截痕为
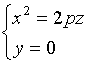
这是一条抛物线，它的轴与轴相重合，顶点为。
用平行于坐标面的平面
与该曲面相截，其截痕为
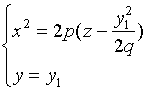
这是一条抛物线，
它的轴平行于轴， 顶点为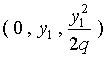
。
4、类似地， 用坐标面
以及平行于
面的平面
去截该曲面时， 其截痕也是抛物线。
综上所述，方程(2)所表示的曲面形状如下
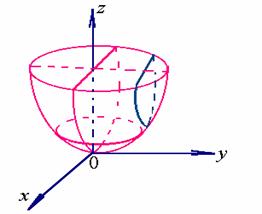
特别地，如果
，那么方程(2)变为
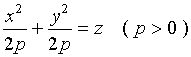
这一曲面可看成是面上的抛物线 
绕轴旋转而成的旋转曲面，这曲面叫做旋转抛物面。
由方程
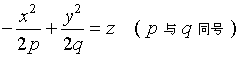
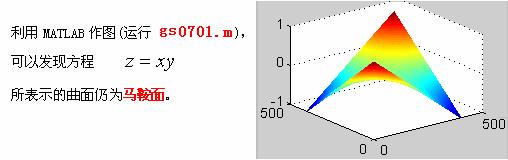
所表示的曲面叫做双曲抛物面或马鞍面。
当 时，它的形状如下图所示
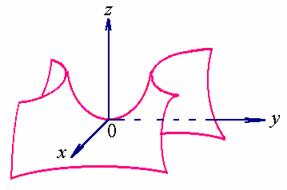
点称之为鞍点。
三、双曲面
由方程
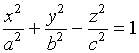(3)
所表示的曲面叫做单叶双曲面。
下面用截痕法来考察它的形状
1、用坐标面与该曲面相截，其截痕为
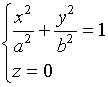
这是一个中心在原点，且半轴分别为与
的椭圆。
2、用平行于面的平面去截曲面，其截痕为
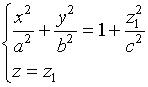
它是中心在轴上，两个半轴分别为
与
的椭圆。
3、用坐标面
与该曲面相截， 其截痕为
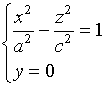
它是中心在原点，实轴为
轴，虚轴为轴的双曲线。
4、用平行于面的平面
去截曲面，其截痕为
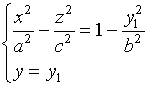
它是中心在
轴，两个半轴的平方为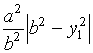
与
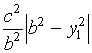的双曲线。
如果
，那么双曲线的实轴平行于轴，虚轴平行于轴。
如果
，那么双曲线的实轴平行于轴，虚轴平行于轴。
如果
，那么平面
去截曲面所得截痕为一对相交于点
的直线，它们是
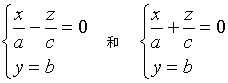
如果
，那么平面
去截曲面所得截痕为一对相交于点
的直线，它们是
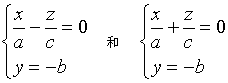
5、类似地，用坐标面和平行于面的平面去截曲面， 所得的截痕也是双曲线，而用平面
去截曲面，其截痕曲线为两对相交的直线。
综上所述， 单叶双曲面的形状如下
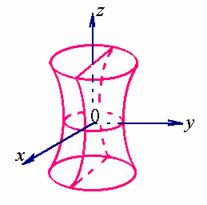
由方程
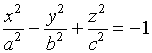(4)
所表示的曲面叫做双叶双曲面。利用截痕法可以判定出它的形状为
